Autoregressive conditional duration

In financial econometrics, an autoregressive conditional duration (ACD, Engle and Russell (1998)) model considers irregularly spaced and autocorrelated intertrade durations. ACD is analogous to GARCH. Indeed, in a continuous double auction (a common trading mechanism in many financial markets) waiting times between two consecutive trades vary at random.

Definition

Specifically, let 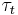$~\tau_t~$ denote the duration (the waiting time between consecutive trades) and assume that 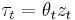$~\tau_t=\theta_t z_t ~$ , where 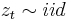$z_t \sim iid~$ , positive and with 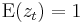$\operatorname{E}(z_t) = 1$ and where the series 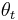$~\theta_t~$ is given by

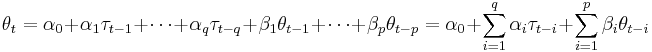
$\theta_t = \alpha_0 %2B \alpha_1 \tau_{t-1} %2B \cdots %2B \alpha_q \tau_{t-q} %2B \beta_1 \theta_{t-1} %2B \cdots %2B \beta_p\theta_{t-p} = \alpha_0 %2B \sum_{i=1}^q \alpha_i \tau_{t-i} %2B \sum_{i=1}^p \beta_i \theta_{t-i}$

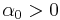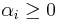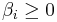and where $~\alpha_0>0~$ , $\alpha_i\ge 0$ , $\beta_i \ge 0$ , $~i>0$ .

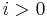References

Robert F. Engle and J.R. Russell. "Autoregressive Conditional Duration: A New Model for Irregularly Spaced Transaction Data", Econometrica, 66:1127-1162, 1998.

N. Hautsch. "Modelling Irregularly Spaced Financial Data", Springer, 2004.